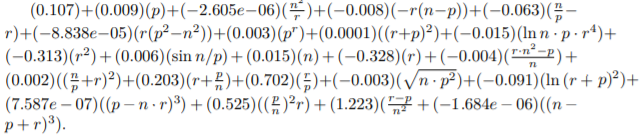
Summer Science Research Project

Facebook Share Twitter Share Email This Article Share on LinkedIn

Estimation and Inference for Correlation Under Censoring

Yilun Cao '22 
Department of Mathematics, Ohio Wesleyan University
Faculty mentor: Scott Linder, Ph.D.

Abstract 

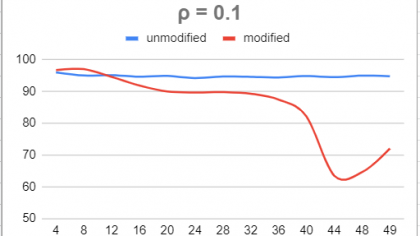
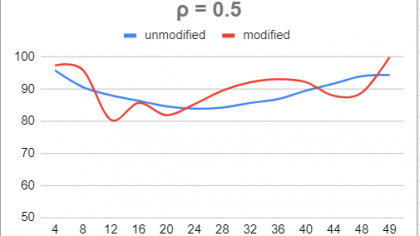
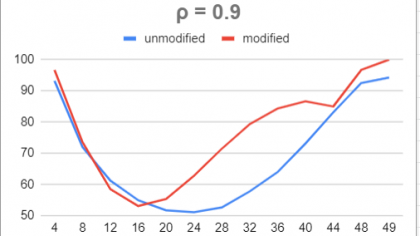
    In many clinical and industrial settings, data are subjected to censoring. Widely used, conventional statistical methods (t-tests, linear regression, etc.) are based on underpinning sampling distributions which typically become mathematically intractable when censoring occurs. Our study examines the effect of censoring on the accuracy of the method for estimating correlation using the Fisher transformation. When censoring is imposed, we observe that actual coverage rates of confidence intervals for the population correlation coefficient constructed through the Fisher Transformation method degrade very rapidly, rendering this method inappropriate. Again using simulation, we propose a shift and scale modification to the approximate normality of the sampling distribution of the Fisher transformed sample correlation. The scale and location shifts are functions of the degree of censoring. This allows us to proposed “modified” confidence intervals for the population correlation under censoring. We observe that these modified intervals offer slight improvement in coverage rate over the unmodified version.

 

All models are wrong, but some models are useful.

George Box

British Statistician 

Background 

    The Fisher Transformation is used to estimate the population correlation coefficient ρ. With r representing the sample correlation, denote the Fisher transformed sample correlation z: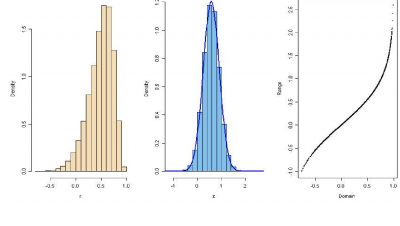 

z=0.5ln((1+r)/(1-r))

     In the full-sample setting (no censoring), the sampling distribution of the z is approximately normal, and this approximation is quite good even for samples as small as n = 8. When p < n observations are made, censoring has occurred. Using simulation we see that this impacts the sampling distribution of z.

METHOD

According to Fisher, (z-f(ρ))/(n-3)1/2 has approximately the Normal distribution with mean 0 and standard deviation 1 in a full sample. We see that this approximation is not reasonable under censoring. Our idea is to rescale and shift the Normal distribution approximation in order to get a better fit.

P(−1.96 < (z − M)/N < 1.96) = .95 or
P(−1.96 · N < z − M < 1.96 · N = .95
We then introduce f(ρ) into the equation,
P(−1.96 · N < z − (M − f(ρ)) − f(ρ) < 1.96 · N) = .95
Let M∗ (n, p, ρ) be a function for M − f(ρ), then
P(−1.96 · N < z − M∗ − f(ρ) < 1.96 · N) = .95

Let E(z) = µz, SD(z) = σz. We see that µz and σz depend on n, p and ρ. Using simulation, we constructed models M(n,p,ρ) is a function for E(z) and N(n,p,ρ) for σz. If the modified normal approximation is appropriate, a 95% confidence interval for f(ρ) can be constructed as a pivotal quantity:

Therefore, a confidence interval for f(ρ) can be constructed using M∗ (n, p, ρ) and N(n, p, ρ) which are models that possibly contain n, p, ρ as predictors: (z − M∗ ) + / − 1.96 · N.

MODELING

Fix n, p, ρ. We first simulated n (x,y) pairs in a sample from a bivariate Normal population and and the right censored the sample to size p, using only the observations corresponding with the p smallest x values. Each sample generates a value of z. We obtained 100,000 simulated values of z for each combination of n, p and ρ . We then built regression functions M∗(n,p,ρ) of µz, and N(n,p,ρ) of σz. M∗ and N have 11 predictors that are the expressions involving n, p, and ρ.

SETTING

Model for M*

Model for N

NOTE

Note that we plug in r instead of ρ when applying M∗ and N in constructing the confidence interval since ρ remains unknown in a practical world.

OUTCOMES

We tested the result by simulating actual confidence levels for nominally 95% confidence intervals, using n=10, 30, and 50 with ρ =0.1, 0.5, 0.9. The plots below demonstrate coverage rates when n is 50.

EVALUATION

1. Coverage rates are lowest and the most unstable when ρ is 0.9 for both methods.
2. Both methods perform well when the size of the sample is small, preferably n ≤ 10.

3. The coverage drops to its lowest faster than the conventional method but also rises faster than it.

4. When ρ is close to zero, modified intervals perform worse than unmodified intervals, but modified intervals do better when ρ is larger. This makes sense because independence should reduce the impact of censoring.